
Evaluate solution importance using incremental ranks
Source:R/eval_rank_importance.R
eval_rank_importance.RdCalculate importance scores for the planning units selected in a solution using an incremental rank procedure (based on Jung et al. 2021).
Usage
eval_rank_importance(
x,
solution,
...,
run_checks = TRUE,
force = FALSE,
by_zone = TRUE,
objective = NULL,
extra_args = NULL,
n,
budgets
)Arguments
- x
problem()object.- solution
numeric,matrix,data.frame,terra::rast(), orsf::sf()object. The argument should be in the same format as the planning unit cost data in the argument tox. See the Solution format section for more information.- ...
not used.
- run_checks
logicalflag indicating whether presolve checks should be run prior solving the problem. These checks are performed using thepresolve_check()function. Defaults toTRUE. Skipping these checks may reduce run time for large problems.- force
logicalflag indicating if an attempt should be made to solve the problem even if potential issues were detected during the presolve checks. Defaults toFALSE.- by_zone
logicalvalue indicating how budgets should be calculated whenxhas multiple zones. IfTRUE, then the incremental rank procedure will increment budgets for each zone separately. IfFALSE, then the incremental rank procedure will increment a single budget that is applied to all zones. Note that this parameter is only considered ifnis specified, and does not affect processing ifbudgetsis specified. Defaults toTRUE.- objective
charactervalue with the name of the objective function that should be used for the incremental rank procedure. This function must be budget limited (e.g., cannot beadd_min_set_objective()). For example,"add_min_shortfall_objective"can be used to specify the minimum shortfall objective (peradd_min_shortfall_objective()). Defaults toNULLsuch that the incremental rank procedure will use the objective specified byx. If using this default andxhas the minimum set objective, then the minimum shortfall objective is used (peradd_min_shortfall_objective()).- extra_args
listwith additional arguments for the objective function (excluding thebudgetparameter). For example, this parameter can be used to supply phylogenetic data for the phylogenetic diversity objective function (i.e., when usingobjective = "add_max_phylo_div_objective"). Defaults toNULLsuch that no additional arguments are supplied.- n
integernumber of increments for the incremental rank procedure. Note that eithernorbudgets(not both) must be specified. Ifnis specified, thenby_zoneis considered during processing for problems with multiple zones.- budgets
numericvector with budget thresholds for each increment in the incremental rank procedure. Note that eithernorbudgets(not both) must be specified.
Value
A numeric, matrix, data.frame,
terra::rast(), or sf::sf() object
containing importance scores for the planning units in the solution.
Specifically, the returned object is in the
same format as the planning unit data in the argument to x.
The object also has the following attributes that provide information
on the incremental rank procedure.
budgetsnumericvector ormatrixcontaining the budgets used for each increment in the incremental rank procedure. If the problem (perx) has a single zone, then the budgets are anumericvector, wherein values correspond to the budgets for each increment. Otherwise, if the problem (perx) has multiple zones, then the budgets are amatrixand their format depends on theby_zoneparameter. Ifby_zone = FALSE, then the budgets are amatrixwith a column for each zone and a row for each budget increment. Alternatively, ifby_zone = TRUE, then thematrixhas a single column and a row for each budget increment.objectivenumericmathematical objective values for each solution generated by the incremental rank procedure.runtimenumerictotal amount of time elapsed (reported in seconds) during the optimization process for each solution generated by the incremental rank procedure.statuscharacterstatus of the optimization process for each solution generated by the incremental rank procedure. Seesolve()for details on interpreting these values.gapnumericvalues describing the optimality gap for each solution generated by the incremental rank procedure. Seesolve()for details on interpreting these values.
Details
Importance scores are calculated using an incremental rank procedure.
Note that if a problem (per x) has complex constraints (i.e.,
constraints that do not involve locking in or locking out planning
units), then the budgets parameter must be specified.
The incremental rank procedure involves the following steps.
A set of budgets are defined. If an argument to the
budgetsparameter is supplied, then the budgets are defined using thebudgets. Otherwise, if an argument to thenparameter is supplied, then the budgets are automatically calculated as a set of values – with equal increments between successive values – that range to a maximum value that is equal to the total cost ofsolution. For example, if considering a problem (perx) with a single zone, a solution with a total cost of 400, andn = 4: then the budgets will be automatically calculated as 100, 200, 300, and 400. If considering a multiple zone problem andby_zone = FALSE, then the budgets will based calculated based on the total cost of thesolutionacross all zones. Otherwise ifby_zone = TRUE, then the budgets are calculated and set based on the total cost of planning units allocated to each zone (separately) in thesolution. Note that after running this function, you can see what budgets were defined by accessing attributes from the result (see below for examples).The problem (per
x) is checked for potential issues. This step is performed to avoid issues during subsequent optimization steps. Note that this step can be skipped usingrun_checks = FALSE. Also, if issues are detected and you wish to proceed anyway, then useforce = TRUEignore any detected issues.The problem is modified for subsequent optimization. In particular, the upper bounds for the planning units in the problem are specified based on the
solution. For problems (perx) that have binary decision types, this step is equivalent to locking out any planning units that are not selected in thesolution. Note that this step is important to ensure that all subsequent optimization processes produce solutions that are nested within thesolution.The problem is further modified for subsequent optimization. Specifically, its objective is overwritten using the objective defined for the incremental rank procedure (per
objective) with the budget defined for the first increment. When this step is repeated during subsequent increments, the objective will be overwritten with with the budget defined for the next increment. Additionally, if an argument to theextra_argsparameter is specified, this argument is used when overwriting the objective.The modified problem is solved to generate a solution. Due to the steps used to modify the problem (i.e., steps 3 and 4), the newly generated solution will contain a subset of the selected planning units in the original
solution.The status of the planning units in the newly generated solution are recorded for later use (e.g., binary values indicating if planning units were selected or not, or the proportion of each planning unit selected) .
The problem is further modified for subsequent optimization. Specifically, the status of the planning units in the newly generated solution are used to set the lower bounds for the planning units in the problem. For problems with binary type decision variables, this step is equivalent to modifying the problem to lock in planning units that were selected by the newly generated solution. Additionally, the newly generated solution is used to specify the starting solution for the subsequent optimization process to reduce processing time (note this is only done when using the CBC or Gurobi solvers).
Steps 4–7 are repeated for each of the remaining budget increments. As increasingly greater budgets are used at higher increments, the modified problem will begin to generate solutions that become increasingly more similar to the original
solution. Note that the status of the planning units in each of these new solutions are recorded for later use.The incremental optimization rank procedure has now completed. The planning unit solution statuses that were previously recorded in each iteration are used to compute relative importance scores. These relative importance scores range between 0 and 1, with higher scores indicating that a given planning unit was selected in earlier increments and is more cost-effective for meeting the objective (per
objective). In particular, for a given planning unit, the importance score is calculated based on the arithmetic mean of the status values. For example, if we performed an incremental rank procedure with five increments and binary decision variables, then a planning unit might have been selected in the second increment. In this example, the planning unit would have the following solution statuses across the five increments: (1st increment) 0, (2nd increment) 1, (3rd increment) 1, (4th increment) 1, and (5th increment) 1. The mean of these values is 0.8, and so the planning unit would have an importance score of 0.8. A score of 0.8 is relatively high, and suggests that this planning unit is highly cost-effective.The importance scores are output in the same format as the planning units in the problem (per
x) (see the Solution Format section for details).
Solution format
Broadly speaking, the argument to solution must be in the same format as
the planning unit data in the argument to x.
Further details on the correct format are listed separately
for each of the different planning unit data formats:
xhasnumericplanning unitsThe argument to
solutionmust be anumericvector with each element corresponding to a different planning unit. It should have the same number of planning units as those in the argument tox. Additionally, any planning units missing cost (NA) values should also have missing (NA) values in the argument tosolution.xhasmatrixplanning unitsThe argument to
solutionmust be amatrixvector with each row corresponding to a different planning unit, and each column correspond to a different management zone. It should have the same number of planning units and zones as those in the argument tox. Additionally, any planning units missing cost (NA) values for a particular zone should also have a missing (NA) values in the argument tosolution.xhasterra::rast()planning unitsThe argument to
solutionbe aterra::rast()object where different cells correspond to different planning units and layers correspond to a different management zones. It should have the same dimensionality (rows, columns, layers), resolution, extent, and coordinate reference system as the planning units in the argument tox. Additionally, any planning units missing cost (NA) values for a particular zone should also have missing (NA) values in the argument tosolution.xhasdata.frameplanning unitsThe argument to
solutionmust be adata.framewith each column corresponding to a different zone, each row corresponding to a different planning unit, and cell values corresponding to the solution value. This means that if adata.frameobject containing the solution also contains additional columns, then these columns will need to be subsetted prior to using this function (see below for example withsf::sf()data). Additionally, any planning units missing cost (NA) values for a particular zone should also have missing (NA) values in the argument tosolution.xhassf::sf()planning unitsThe argument to
solutionmust be asf::sf()object with each column corresponding to a different zone, each row corresponding to a different planning unit, and cell values corresponding to the solution value. This means that if thesf::sf()object containing the solution also contains additional columns, then these columns will need to be subsetted prior to using this function (see below for example). Additionally, the argument tosolutionmust also have the same coordinate reference system as the planning unit data. Furthermore, any planning units missing cost (NA) values for a particular zone should also have missing (NA) values in the argument tosolution.
References
Jung M, Arnell A, de Lamo X, García-Rangel S, Lewis M, Mark J, Merow C, Miles L, Ondo I, Pironon S, Ravilious C, Rivers M, Schepaschenko D, Tallowin O, van Soesbergen A, Govaerts R, Boyle BL, Enquist BJ, Feng X, Gallagher R, Maitner B, Meiri S, Mulligan M, Ofer G, Roll U, Hanson JO, Jetz W, Di Marco M, McGowan J, Rinnan DS, Sachs JD, Lesiv M, Adams VM, Andrew SC, Burger JR, Hannah L, Marquet PA, McCarthy JK, Morueta-Holme N, Newman EA, Park DS, Roehrdanz PR, Svenning J-C, Violle C, Wieringa JJ, Wynne G, Fritz S, Strassburg BBN, Obersteiner M, Kapos V, Burgess N, Schmidt- Traub G, Visconti P (2021) Areas of global importance for conserving terrestrial biodiversity, carbon and water. Nature Ecology and Evolution, 5: 1499–1509.
See also
Other functions for evaluating solution importance:
eval_ferrier_importance(),
eval_rare_richness_importance(),
eval_replacement_importance()
Examples
# \dontrun{
# seed seed for reproducibility
set.seed(600)
# load data
sim_pu_raster <- get_sim_pu_raster()
sim_pu_polygons <- get_sim_pu_polygons()
sim_features <- get_sim_features()
sim_zones_pu_raster <- get_sim_zones_pu_raster()
sim_zones_features <- get_sim_zones_features()
# create minimal problem with binary decisions
p1 <-
problem(sim_pu_raster, sim_features) %>%
add_min_set_objective() %>%
add_relative_targets(0.1) %>%
add_binary_decisions() %>%
add_default_solver(gap = 0, verbose = FALSE)
# solve problem
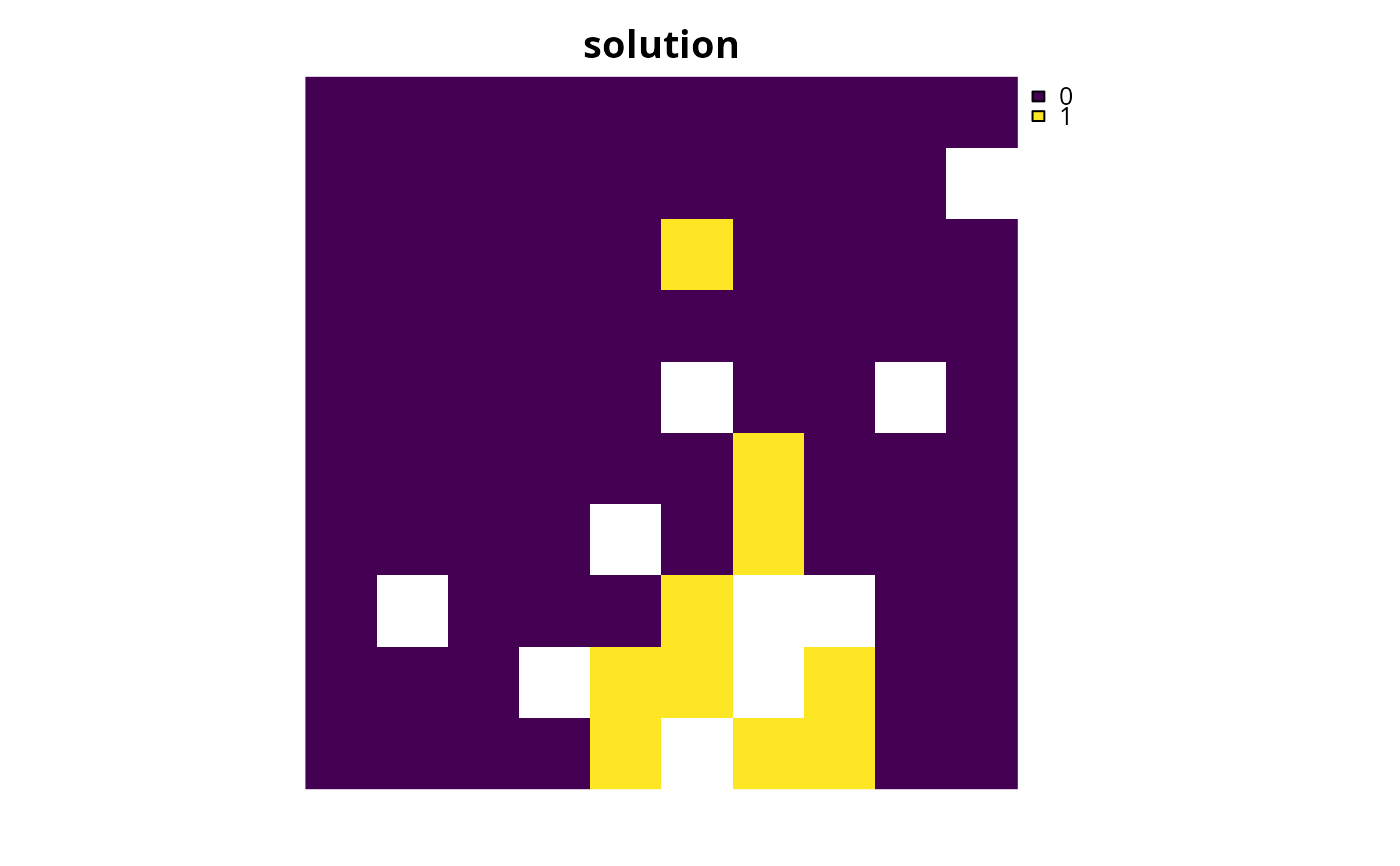
s1 <- solve(p1)
# print solution
print(s1)
#> class : SpatRaster
#> size : 10, 10, 1 (nrow, ncol, nlyr)
#> resolution : 0.1, 0.1 (x, y)
#> extent : 0, 1, 0, 1 (xmin, xmax, ymin, ymax)
#> coord. ref. : Undefined Cartesian SRS
#> source(s) : memory
#> varname : sim_pu_raster
#> name : layer
#> min value : 0
#> max value : 1
# plot solution
plot(s1, main = "solution", axes = FALSE)
 # calculate importance scores using 10 budget increments
# N.B. since the objective for the incremental rank procedure is not
# explicitly defined and the problem has a minimum set objective, the
# the minimum shortfall objective is used by default
rs1 <- eval_rank_importance(p1, s1, n = 10)
# print importance scores
print(rs1)
#> class : SpatRaster
#> size : 10, 10, 1 (nrow, ncol, nlyr)
#> resolution : 0.1, 0.1 (x, y)
#> extent : 0, 1, 0, 1 (xmin, xmax, ymin, ymax)
#> coord. ref. : Undefined Cartesian SRS
#> source(s) : memory
#> varname : sim_pu_raster
#> name : rs
#> min value : 0
#> max value : 1
# plot importance scores
plot(rs1, main = "rank importance (10, min shortfall obj", axes = FALSE)
# calculate importance scores using 10 budget increments
# N.B. since the objective for the incremental rank procedure is not
# explicitly defined and the problem has a minimum set objective, the
# the minimum shortfall objective is used by default
rs1 <- eval_rank_importance(p1, s1, n = 10)
# print importance scores
print(rs1)
#> class : SpatRaster
#> size : 10, 10, 1 (nrow, ncol, nlyr)
#> resolution : 0.1, 0.1 (x, y)
#> extent : 0, 1, 0, 1 (xmin, xmax, ymin, ymax)
#> coord. ref. : Undefined Cartesian SRS
#> source(s) : memory
#> varname : sim_pu_raster
#> name : rs
#> min value : 0
#> max value : 1
# plot importance scores
plot(rs1, main = "rank importance (10, min shortfall obj", axes = FALSE)
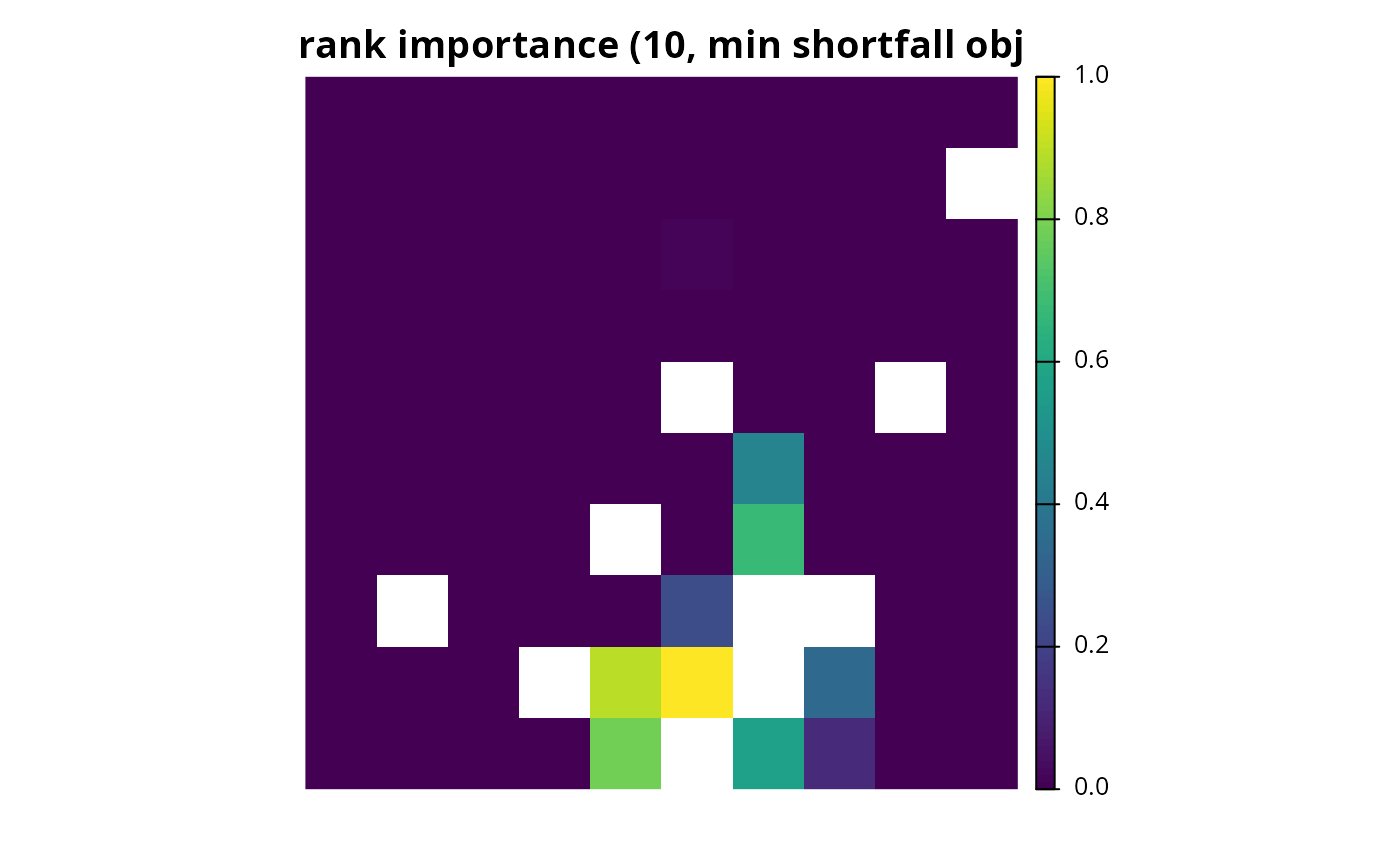 # display optimization information from the attributes
## status
print(attr(rs1, "status"))
#> [1] "OPTIMAL" "OPTIMAL" "OPTIMAL" "OPTIMAL" "OPTIMAL" "OPTIMAL" "OPTIMAL"
#> [8] "OPTIMAL" "OPTIMAL" "OPTIMAL"
## optimality gap
print(attr(rs1, "gap"))
#> [1] 0 0 0 0 0 0 0 0 0 0
## run time
print(attr(rs1, "runtime"))
#> [1] 0.002 0.002 0.002 0.002 0.002 0.002 0.002 0.002 0.002 0.002
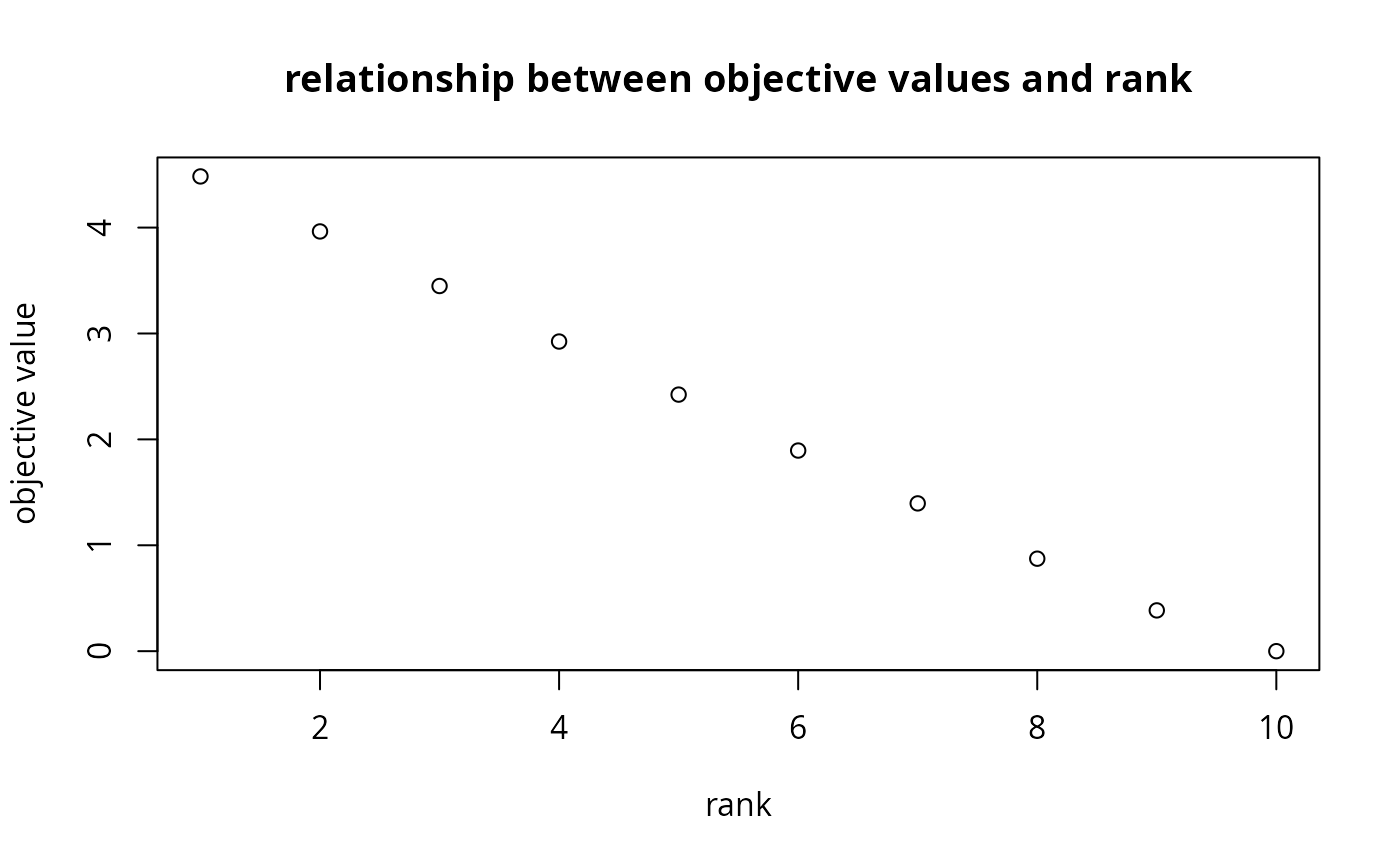
## objective value
print(attr(rs1, "objective"))
#> [1] 4.4831422 3.9636924 3.4483566 2.9239906 2.4229403 1.8946389 1.3955220
#> [8] 0.8733925 0.3850706 0.0000000
# plot relationship between objective values and budget increment
plot(
y = attr(rs1, "objective"),
x = seq_along(attr(rs1, "objective")),
ylab = "objective value", xlab = "budget increment",
main = "Relationship between objective values and budget increment"
)
# display optimization information from the attributes
## status
print(attr(rs1, "status"))
#> [1] "OPTIMAL" "OPTIMAL" "OPTIMAL" "OPTIMAL" "OPTIMAL" "OPTIMAL" "OPTIMAL"
#> [8] "OPTIMAL" "OPTIMAL" "OPTIMAL"
## optimality gap
print(attr(rs1, "gap"))
#> [1] 0 0 0 0 0 0 0 0 0 0
## run time
print(attr(rs1, "runtime"))
#> [1] 0.002 0.002 0.002 0.002 0.002 0.002 0.002 0.002 0.002 0.002
## objective value
print(attr(rs1, "objective"))
#> [1] 4.4831422 3.9636924 3.4483566 2.9239906 2.4229403 1.8946389 1.3955220
#> [8] 0.8733925 0.3850706 0.0000000
# plot relationship between objective values and budget increment
plot(
y = attr(rs1, "objective"),
x = seq_along(attr(rs1, "objective")),
ylab = "objective value", xlab = "budget increment",
main = "Relationship between objective values and budget increment"
)
 # calculate importance scores using the maximum utility objective and
# based on 10 different budgets
rs2 <- eval_rank_importance(
p1, s1, n = 10, objective = "add_max_utility_objective"
)
#> Warning: `problem()` has an objective that does not support targets.
#> ℹ The specified targets will be ignored during optimization.
#> ℹ If the targets are important, then use a different objective.
# print importance scores
print(rs2)
#> class : SpatRaster
#> size : 10, 10, 1 (nrow, ncol, nlyr)
#> resolution : 0.1, 0.1 (x, y)
#> extent : 0, 1, 0, 1 (xmin, xmax, ymin, ymax)
#> coord. ref. : Undefined Cartesian SRS
#> source(s) : memory
#> varname : sim_pu_raster
#> name : rs
#> min value : 0
#> max value : 1
# plot importance scores
plot(rs2, main = "rank importance (10, max utility obj)", axes = FALSE)
# calculate importance scores using the maximum utility objective and
# based on 10 different budgets
rs2 <- eval_rank_importance(
p1, s1, n = 10, objective = "add_max_utility_objective"
)
#> Warning: `problem()` has an objective that does not support targets.
#> ℹ The specified targets will be ignored during optimization.
#> ℹ If the targets are important, then use a different objective.
# print importance scores
print(rs2)
#> class : SpatRaster
#> size : 10, 10, 1 (nrow, ncol, nlyr)
#> resolution : 0.1, 0.1 (x, y)
#> extent : 0, 1, 0, 1 (xmin, xmax, ymin, ymax)
#> coord. ref. : Undefined Cartesian SRS
#> source(s) : memory
#> varname : sim_pu_raster
#> name : rs
#> min value : 0
#> max value : 1
# plot importance scores
plot(rs2, main = "rank importance (10, max utility obj)", axes = FALSE)
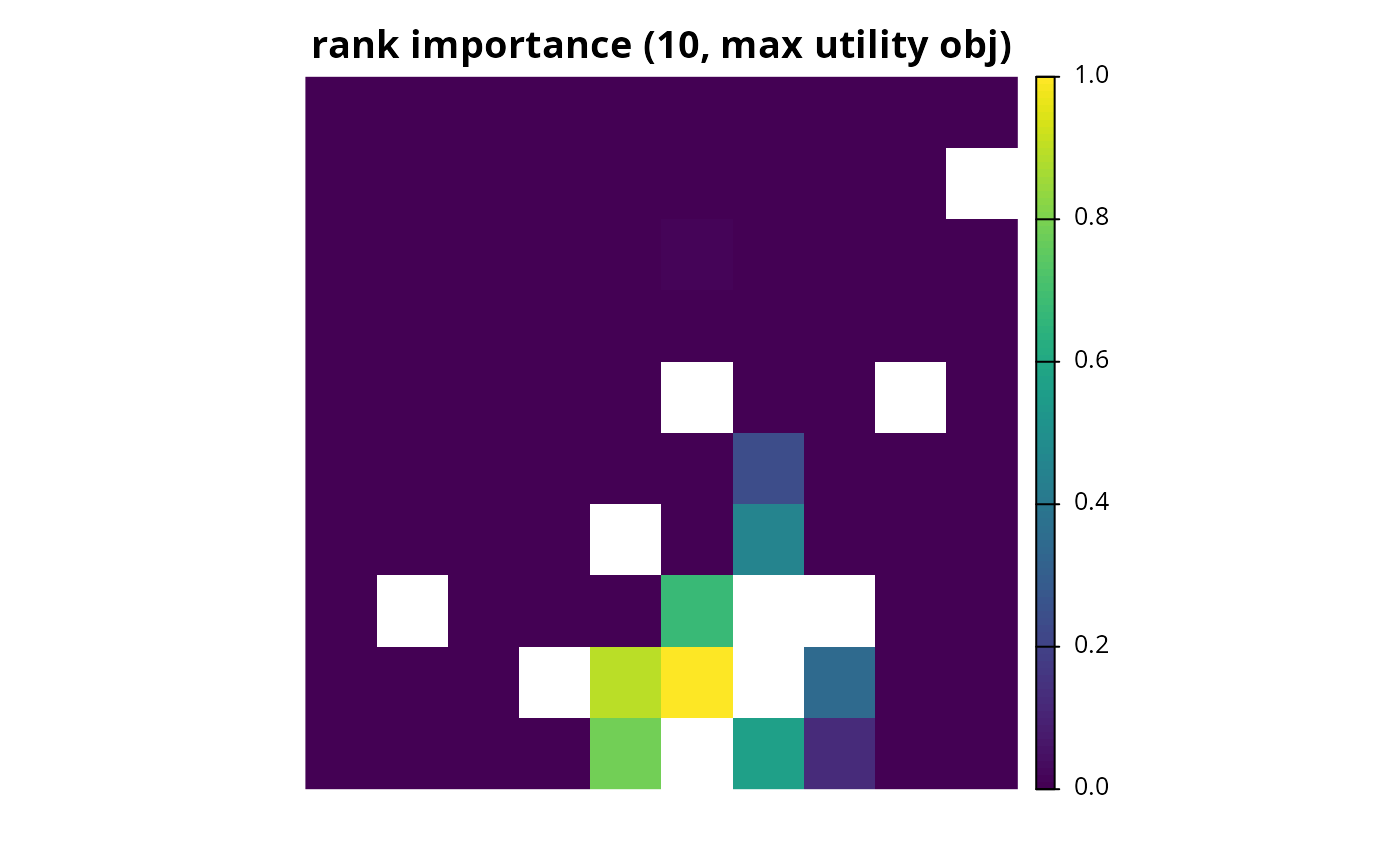 # calculate importance scores based on 5 manually specified budgets
# calculate 5 ranks using equal intervals
# N.B. we use length.out = 6 because we want 5 budgets > 0
budgets <- seq(0, eval_cost_summary(p1, s1)$cost[[1]], length.out = 6)[-1]
# calculate importance using manually specified budgets
# N.B. since the objective is not explicitly defined and the problem has a
# minimum set objective, the minimum shortfall objective is used by default
rs3 <- eval_rank_importance(p1, s1, budgets = budgets)
# print importance scores
print(rs3)
#> class : SpatRaster
#> size : 10, 10, 1 (nrow, ncol, nlyr)
#> resolution : 0.1, 0.1 (x, y)
#> extent : 0, 1, 0, 1 (xmin, xmax, ymin, ymax)
#> coord. ref. : Undefined Cartesian SRS
#> source(s) : memory
#> varname : sim_pu_raster
#> name : rs
#> min value : 0
#> max value : 1
# plot importance scores
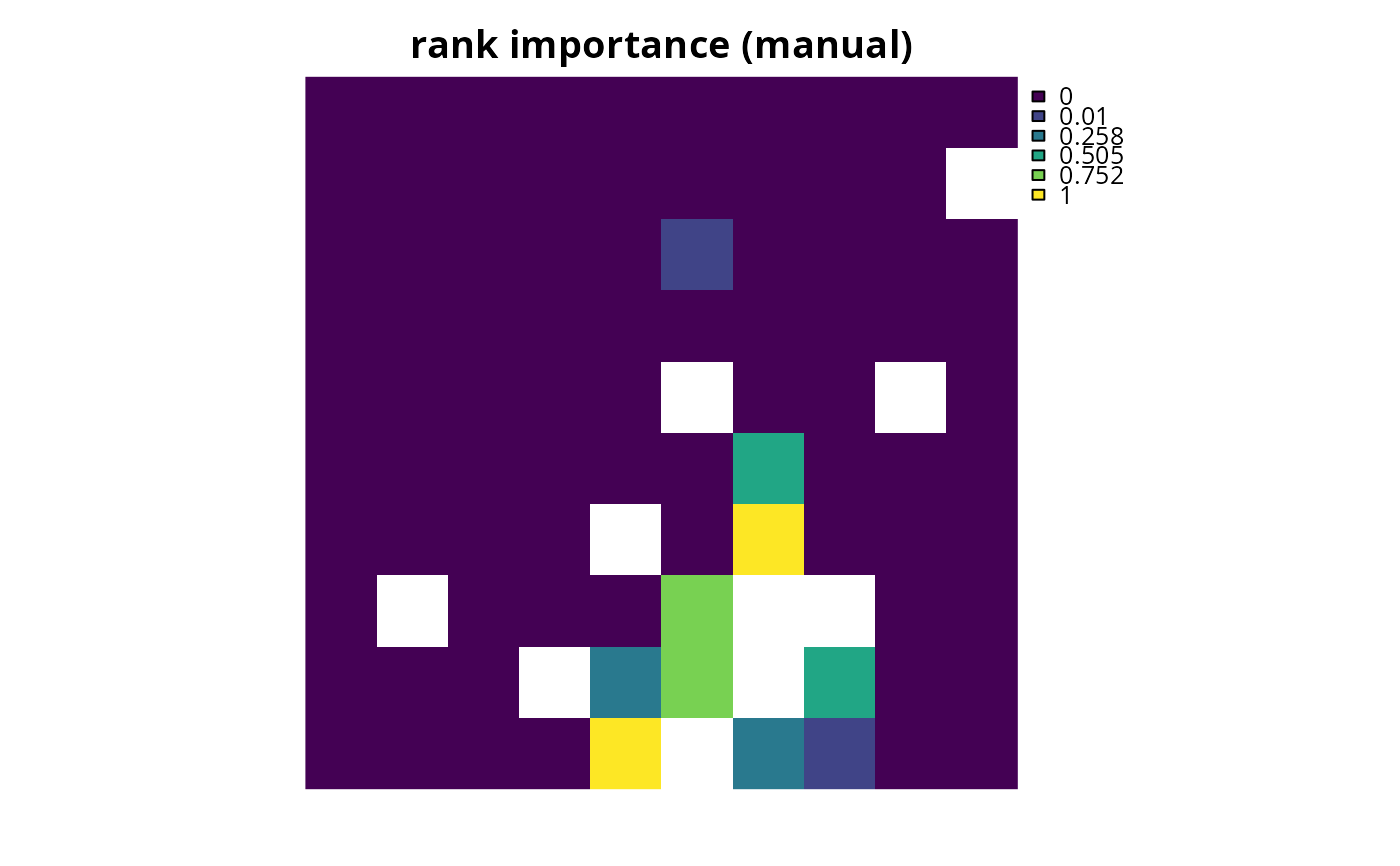
plot(rs3, main = "rank importance (manual)", axes = FALSE)
# calculate importance scores based on 5 manually specified budgets
# calculate 5 ranks using equal intervals
# N.B. we use length.out = 6 because we want 5 budgets > 0
budgets <- seq(0, eval_cost_summary(p1, s1)$cost[[1]], length.out = 6)[-1]
# calculate importance using manually specified budgets
# N.B. since the objective is not explicitly defined and the problem has a
# minimum set objective, the minimum shortfall objective is used by default
rs3 <- eval_rank_importance(p1, s1, budgets = budgets)
# print importance scores
print(rs3)
#> class : SpatRaster
#> size : 10, 10, 1 (nrow, ncol, nlyr)
#> resolution : 0.1, 0.1 (x, y)
#> extent : 0, 1, 0, 1 (xmin, xmax, ymin, ymax)
#> coord. ref. : Undefined Cartesian SRS
#> source(s) : memory
#> varname : sim_pu_raster
#> name : rs
#> min value : 0
#> max value : 1
# plot importance scores
plot(rs3, main = "rank importance (manual)", axes = FALSE)
 # build multi-zone conservation problem with raster data
p4 <-
problem(sim_zones_pu_raster, sim_zones_features) %>%
add_min_set_objective() %>%
add_relative_targets(matrix(runif(15, 0.1, 0.2), nrow = 5, ncol = 3)) %>%
add_binary_decisions() %>%
add_default_solver(gap = 0, verbose = FALSE)
# solve the problem
s4 <- solve(p4)
names(s4) <- paste0("zone ", seq_len(terra::nlyr(sim_zones_pu_raster)))
# print solution
print(s4)
#> class : SpatRaster
#> size : 10, 10, 3 (nrow, ncol, nlyr)
#> resolution : 0.1, 0.1 (x, y)
#> extent : 0, 1, 0, 1 (xmin, xmax, ymin, ymax)
#> coord. ref. : Undefined Cartesian SRS
#> source(s) : memory
#> varnames : sim_zones_pu_raster
#> sim_zones_pu_raster
#> sim_zones_pu_raster
#> names : zone 1, zone 2, zone 3
#> min values : 0, 0, 0
#> max values : 1, 1, 1
# plot solution
# each panel corresponds to a different zone, and data show the
# status of each planning unit in a given zone
plot(s4, axes = FALSE)
# build multi-zone conservation problem with raster data
p4 <-
problem(sim_zones_pu_raster, sim_zones_features) %>%
add_min_set_objective() %>%
add_relative_targets(matrix(runif(15, 0.1, 0.2), nrow = 5, ncol = 3)) %>%
add_binary_decisions() %>%
add_default_solver(gap = 0, verbose = FALSE)
# solve the problem
s4 <- solve(p4)
names(s4) <- paste0("zone ", seq_len(terra::nlyr(sim_zones_pu_raster)))
# print solution
print(s4)
#> class : SpatRaster
#> size : 10, 10, 3 (nrow, ncol, nlyr)
#> resolution : 0.1, 0.1 (x, y)
#> extent : 0, 1, 0, 1 (xmin, xmax, ymin, ymax)
#> coord. ref. : Undefined Cartesian SRS
#> source(s) : memory
#> varnames : sim_zones_pu_raster
#> sim_zones_pu_raster
#> sim_zones_pu_raster
#> names : zone 1, zone 2, zone 3
#> min values : 0, 0, 0
#> max values : 1, 1, 1
# plot solution
# each panel corresponds to a different zone, and data show the
# status of each planning unit in a given zone
plot(s4, axes = FALSE)
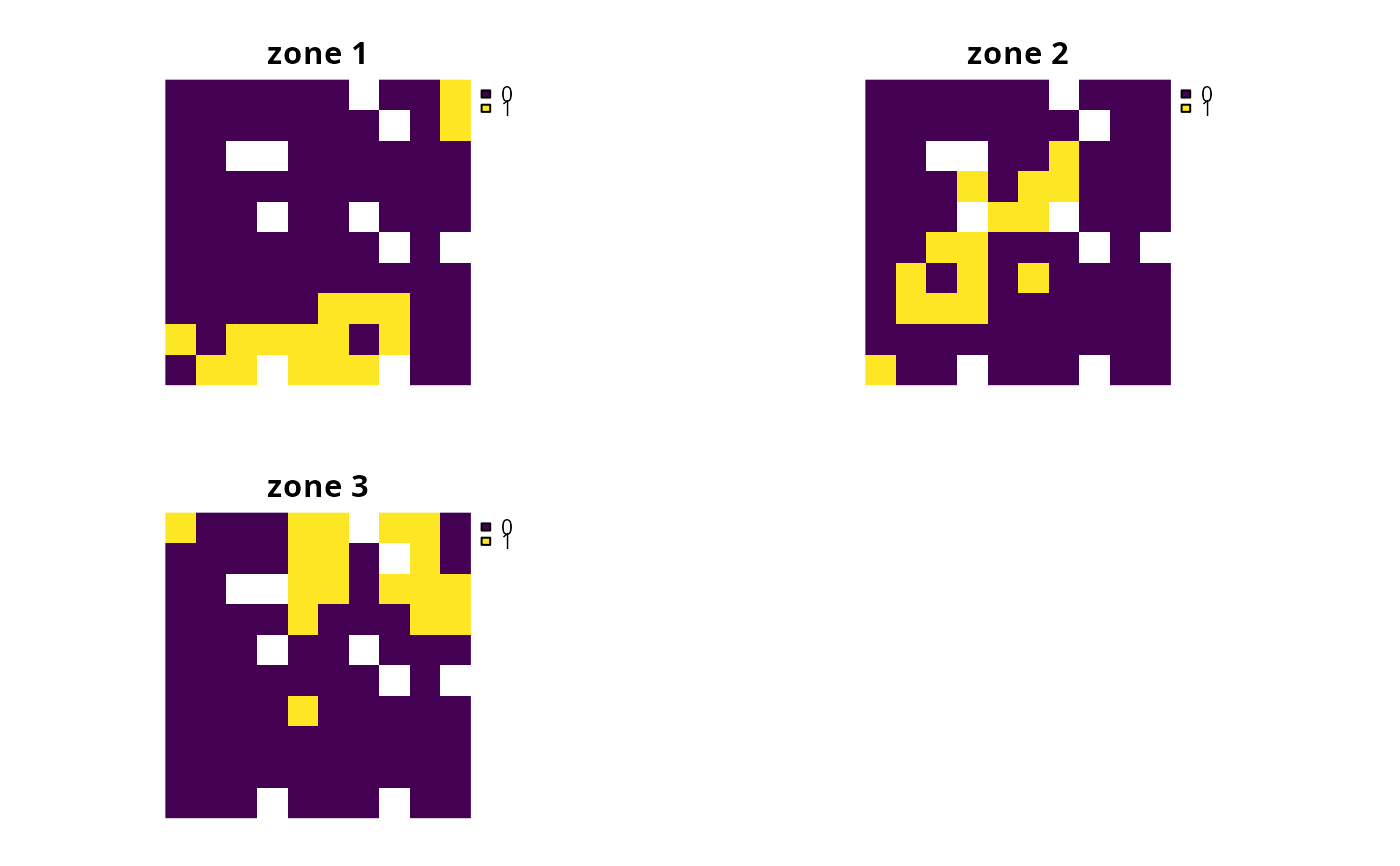 # calculate importance scores
rs4 <- eval_rank_importance(p4, s4, n = 5)
names(rs4) <- paste0("zone ", seq_len(terra::nlyr(sim_zones_pu_raster)))
# plot importance
# each panel corresponds to a different zone, and data show the
# importance of each planning unit in a given zone
plot(rs4, axes = FALSE)
# calculate importance scores
rs4 <- eval_rank_importance(p4, s4, n = 5)
names(rs4) <- paste0("zone ", seq_len(terra::nlyr(sim_zones_pu_raster)))
# plot importance
# each panel corresponds to a different zone, and data show the
# importance of each planning unit in a given zone
plot(rs4, axes = FALSE)
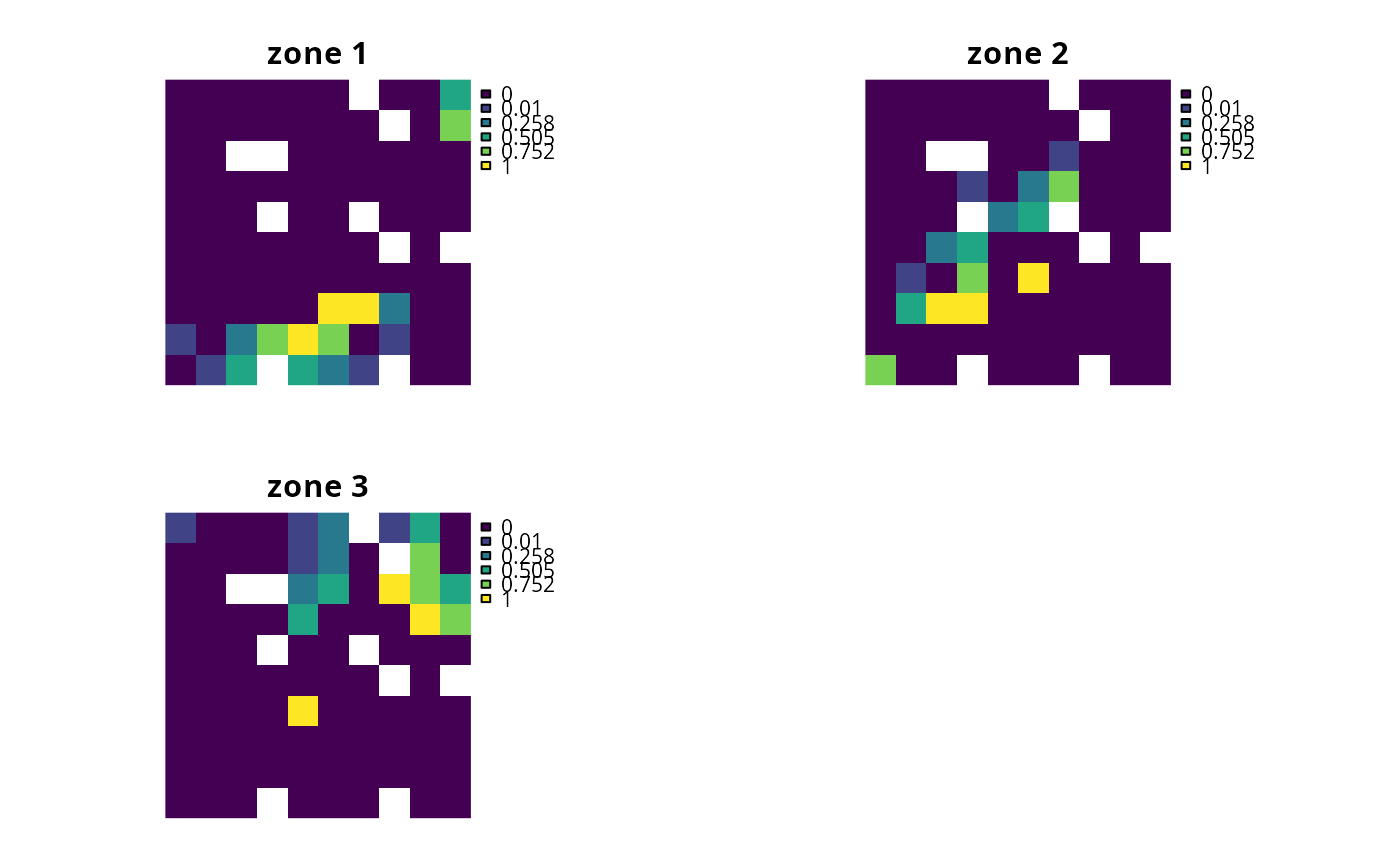 # }
# }