Add relative targets

Set targets as a proportion (between 0 and 1) of the maximum level of representation of features in the study area. Please note that proportions are scaled according to the features' total abundances in the study area (including any locked out planning units, or planning units with NA cost values) using the feature_abundances() function.

Usage

add_relative_targets(x, targets)

# S4 method for class 'ConservationProblem,numeric'
add_relative_targets(x, targets)

# S4 method for class 'ConservationProblem,matrix'
add_relative_targets(x, targets)

# S4 method for class 'ConservationProblem,character'
add_relative_targets(x, targets)

Arguments

x: problem() object.
targets: Object that specifies the targets for each feature. See the Targets format section for more information.

Value

An updated problem() object with the targets added to it.

Details

Targets are used to specify the minimum amount or proportion of a feature's distribution that needs to be protected. Most conservation planning problems require targets with the exception of the maximum cover (see add_max_cover_objective()) and maximum utility (see add_max_utility_objective()) problems. Attempting to solve problems with objectives that require targets without specifying targets will throw an error.

For problems associated with multiple management zones, add_absolute_targets() can be used to set targets that each pertain to a single feature and a single zone. To set targets that can be met through allocating different planning units to multiple zones, see the add_manual_targets() function. An example of a target that could be met through allocations to multiple zones might be where each management zone is expected to result in a different amount of a feature and the target requires that the total amount of the feature in all zones must exceed a certain threshold. In other words, the target does not require that any single zone secure a specific amount of the feature, but the total amount held in all zones must secure a specific amount. Thus the target could, potentially, be met through allocating all planning units to any specific management zone, or through allocating the planning units to different combinations of management zones.

Targets format

The targets for a problem can be specified using the following formats.

targets as a numeric vector: containing target values for each feature. Additionally, for convenience, this format can be a single value to assign the same target to each feature. Note that this format cannot be used to specify targets for problems with multiple zones.
targets as a matrix object: containing a target for each feature in each zone. Here, each row corresponds to a different feature in argument to x, each column corresponds to a different zone in argument to x, and each cell contains the target value for a given feature that the solution needs to secure in a given zone.
targets as a character vector: containing the column name(s) in the feature data associated with the argument to x that contain targets. This format can only be used when the feature data associated with x is a sf::st_sf() or data.frame. For problems that contain a single zone, the argument to targets must contain a single column name. Otherwise, for problems that contain multiple zones, the argument to targets must contain a column name for each zone.

Examples

# \dontrun{
# set seed for reproducibility
set.seed(500)
sim_pu_raster <- get_sim_pu_raster()
sim_features <- get_sim_features()
sim_zones_pu_raster <- get_sim_zones_pu_raster()
sim_zones_features <- get_sim_zones_features()

# create base problem
p <-
  problem(sim_pu_raster, sim_features) %>%
  add_min_set_objective() %>%
  add_binary_decisions() %>%
  add_default_solver(verbose = FALSE)

# create problem with 10% targets
p1 <- p %>% add_relative_targets(0.1)

# create problem with varying targets for each feature
targets <- c(0.1, 0.2, 0.3, 0.4, 0.5)
p2 <- p %>% add_relative_targets(targets)

# solve problem
s3 <- c(solve(p1), solve(p2))
names(s3) <- c("10% targets", "varying targets")

# plot solution
plot(s3, main = , axes = FALSE)


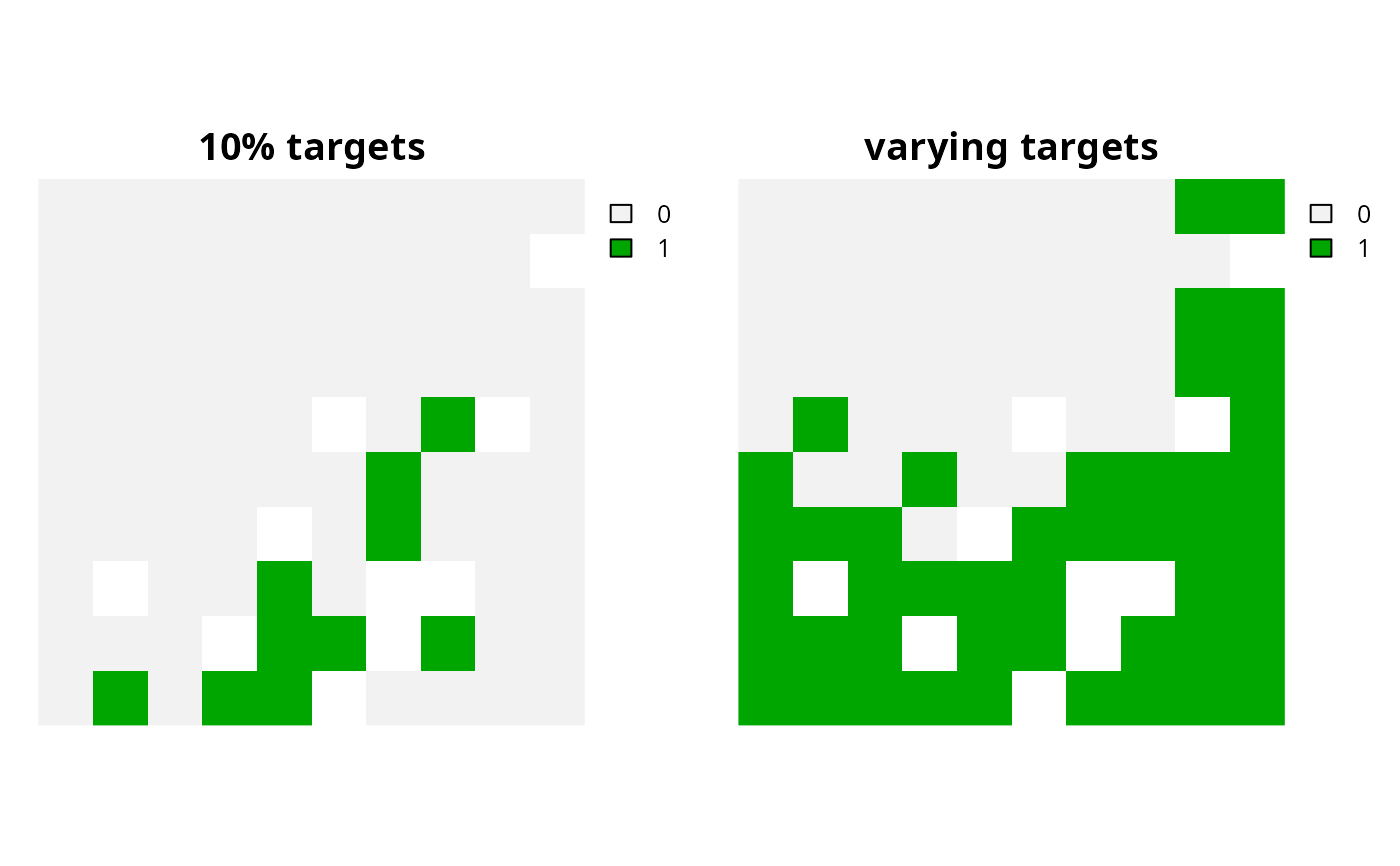# create a problem with multiple management zones
p4 <-
  problem(sim_zones_pu_raster, sim_zones_features) %>%
  add_min_set_objective() %>%
  add_binary_decisions() %>%
  add_default_solver(verbose = FALSE)

# create a problem with targets that specify an equal amount of each feature
# to be represented in each zone
p4_targets <- matrix(
  0.1, nrow = 5, ncol = 3, dimnames = list(
    feature_names(sim_zones_features), zone_names(sim_zones_features)
  )
)
print(p4_targets)
#>           zone_1 zone_2 zone_3
#> feature_1    0.1    0.1    0.1
#> feature_2    0.1    0.1    0.1
#> feature_3    0.1    0.1    0.1
#> feature_4    0.1    0.1    0.1
#> feature_5    0.1    0.1    0.1

p5 <- p4 %>% add_relative_targets(p4_targets)

# solve problem
s5 <- solve(p5)

# plot solution (cell values correspond to zone identifiers)
plot(category_layer(s5), main = "equal targets")


# create a problem with targets that require a varying amount of each
# feature to be represented in each zone
p6_targets <- matrix(
  runif(15, 0.01, 0.2), nrow = 5, ncol = 3, dimnames = list(
    feature_names(sim_zones_features), zone_names(sim_zones_features)
  )
)
print(p6_targets)
#>               zone_1     zone_2     zone_3
#> feature_1 0.16838399 0.04908221 0.06359158
#> feature_2 0.14775224 0.10731456 0.17964011
#> feature_3 0.19530969 0.18583855 0.15529418
#> feature_4 0.09884473 0.16747797 0.04122594
#> feature_5 0.16433284 0.14519964 0.14909414

p6 <- p4 %>% add_relative_targets(p6_targets)

# solve problem
s6 <- solve(p6)

# plot solution (cell values correspond to zone identifiers)
plot(category_layer(s6), main = "varying targets")

# }