Add representation targets

Targets are used to specify the minimum amount or proportion of a feature's distribution that should (ideally) be covered (represented) by a solution. Most objectives require targets, and attempting to solve a problem that requires targets and does not have them specified will result in an error.

Details

The following functions can be used to add targets to a conservation planning problem(). For further information on these functions, see the Usage section below. Also, note that if multiple of these functions are added to a problem(), then only the last function added will be used.

add_auto_targets(): Add targets based on a particular target setting method.
add_group_targets(): Add targets wherein each feature is assigned to a particular group and a target setting method is specified for each feature group.
add_relative_targets(): Add targets expressed as a proportion (between 0 and 1) of the maximum level of representation of each feature in the study area.
add_absolute_targets(): Add targets expressed as the same values as the underlying feature data (ignoring any specified feature units).
add_manual_targets(): Add targets by manually specifying all the required information for each target. This function can be used customize all aspects of a target and is especially useful when working with multiple zones.

Target setting

Many conservation planning problems require targets. Targets are used to specify the minimum amount, or proportion, of a feature's spatial distribution that should ideally be protected. This is important so that the optimization process can weigh the merits and trade-offs between improving the representation of one feature over another feature. Although it can be challenging to set meaningful targets, this is a critical step for ensuring that prioritizations meet the stakeholder objectives that underpin a prioritization exercise (Carwardine et al. 2009). In other words, targets play an important role in ensuring that a priority setting process is properly tuned according to stakeholder requirements. For example, targets provide a mechanism for ensuring that a prioritization secures enough habitat to promote the long-term persistence of each threatened species, culturally important species, or economically important ecosystem services under consideration. Since there is often uncertainty regarding stakeholder objectives (e.g., how much habitat should be protected for a given species) or the influence of particular target on a prioritization (e.g., how would setting a 90% or 100% for a threatened species alter priorities), it is often useful to generate and compare a suite of prioritizations based on different target scenarios.

Usage

A variety of functions can be used to specify targets for a conservation planning problem. Below we describe them in detail.

The add_auto_targets() function can be used to add targets to a conservation planning problem. It provides a flexible interface for specifying targets based on a single method, or a combination of methods. Note that this function is specifically designed for problems that have a single zone, and cannot be used for problems that have multiple zones. For example, given problem x, it could be used to specify targets for all features calculated following Jung et al. (2021) with the following code.
```
# specify targets based on default parameters via method name
x %>% add_auto_targets(method = "jung")

# specify targets based on default parameters via function
x %>% add_auto_targets(method = spec_jung_targets())

# specify targets based on customized parameters via function
x %>% add_auto_targets(method = spec_jung_targets(prop_uplift = 0.05))
```
Additionally, if x had three features – with the first feature corresponding to an ecosystem and the latter two to different species – this function could be used to specify a target for the ecosystem feature based on Polak et al. (2015) and targets for the species features based on Jung et al. (2021) with the following code.
```
# specify target setting methods for each feature with default parameters
# via method name
x %>% add_auto_targets(
  method = list("polak", "jung", "jung")
)

# specify target setting methods for each feature with customized parameters
# via functions
x %>% add_auto_targets(
  method = list(
    spec_polak_targets(),
    spec_jung_targets(prop_uplift = 0.05),
    spec_jung_targets(prop_uplift = 0.07)
  )
)
```
Targets can also be specified based on the maximum or minimum of multiple other target setting methods. For example, targets can be specified as the maximum of the Polak et al. (2015) and Jung et al. (2021) target setting methodologies with the following code:
```
x %>% add_auto_targets(
  method = spec_max_targets(spec_polak_targets(), spec_jung_targets())
)
```
The following functions can be used to specify targets in conjunction with the add_auto_targets() function. Note that some of these functions do not have default parameters for all arguments and, as such, cannot be specified using their name (e.g., method = "relative" will not work because spec_relative_targets() requires the user to specify an argument for the targets parameter).

spec_relative_targets()

Specify targets expressed as a proportion (between 0 and 1) of the total amount of each feature.

spec_absolute_targets()

Specify targets expressed as the same values as the underlying feature data (ignoring any specified feature units).

spec_area_targets()

Specify targets expressed as area-based units.

spec_interp_absolute_targets()

Specify targets based on an interpolation procedure between thresholds expressed as the same values as the underlying feature data (ignoring any specified feature units).

spec_interp_area_targets()

Specify targets based on an interpolation procedure between area-based thresholds.

spec_pop_size_targets()

Specify targets based on minimum population sizes.

spec_rule_targets()

Specify targets calculated following a rule-based procedure based on a set of ecological and ecosystem criteria. This is a customizable version of the approach in Harris and Holness (2023).

spec_rl_species_targets()

Specify targets based on criteria from the International Union for the Conservation of Nature (IUCN) Red List of Threatened Species (IUCN 2025).

spec_rl_ecosystem_targets()

Specify targets based on criteria from the International Union for the Conservation of Nature (IUCN) Red List of Ecosystems (IUCN 2024).

spec_duran_targets()

Specify targets following Durán et al. (2020).

spec_jung_targets()

Specify targets following Jung et al. (2021).

spec_polak_targets()

Specify targets following Polak et al. (2015).

spec_rodrigues_targets()

Specify targets following Rodrigues et al. (2004).

spec_ward_targets()

Specify targets following Ward et al. (2025).

spec_wilson_targets()

Specify targets following Wilson et al. (2010).

spec_watson_targets()

Specify targets following Watson et al. (2010).

spec_min_targets()

Specify targets based on the minimum of other target setting methods.

spec_max_targets()

Specify targets based on the maximum of other target setting methods.
The add_group_targets() function provides a convenient interface for adding targets to a conservation planning problem based on groups. By assigning each feature to a group and then specifying a target setting method for each group, it can be used to assign targets for features based on different target setting methods. This function is designed to be used in conjunction with the previously described functions specifying targets for the add_auto_targets() function (e.g., spec_relative_targets(), spec_absolute_targets(), spec_jung_targets()). Note that this function is specifically designed for problems that have a single zone, and cannot be used for problems that have multiple zones. For example, if the problem x had three features – with the first feature corresponding to an ecosystem and the latter two to different species – this function could be used to set targets for the ecosystem feature based on Polak et al. (2015) and targets for the species features based on Jung et al. (2021) with the following code.
```
# specify target setting methods for groups with default parameters
# via method names
x %>% add_group_targets(
  group = c("eco", "spp", "spp"),
  list(eco = "polak", spp = "jung")
)

# specify target setting methods for groups with default parameters
# via functions
x %>% add_group_targets(
  group = c("eco", "spp", "spp"),
  list(eco = spec_polak_targets(), spp = spec_jung_targets())
)

# specify target setting methods for groups with customized parameters
# via functions
x %>% add_group_targets(
  group = c("eco", "spp", "spp"),
  list(
    eco = spec_polak_targets(),
    spp = spec_jung_targets(prop_uplift = 0.05)
  )
)
```
A set of additional functions are available for adding targets directly to a conservation planning problem. These functions are especially useful when target thresholds have been pre-computed, or when considering problems that have multiple zones. In particular, the following functions are available.

add_relative_targets()

Add targets expressed as a proportion (between 0 and 1) of the total amount of each feature. Note that this function provides a convenient alternative to spec_relative_targets().

add_absolute_targets()

Add targets expressed as the same values as the underlying feature data (ignoring any specified feature units). Note that this function provides a convenient alternative to spec_absolute_targets().

add_manual_targets()

Add targets to a conservation planning problem by manually specifying all the required information for each target. This function is especially useful for problems that have multiple zones because it can be used to specify, for a given feature, which zone – or combination of zones – should be considered for assessing feature representation. In addition to specifying targets where feature representation should ideally be greater than or equal to target thresholds (i.e., as is the case for all other target setting functions), this function provides the functionality to specify targets where feature representation should be smaller than or equal to – or equal to – target thresholds (i.e., the constraint sense for the target).

References

Durán AP, Green JMH, West CD, Visconti P, Burgess ND, Virah‐Sawmy M, Balmford A (2020) A practical approach to measuring the biodiversity impacts of land conversion. Methods in Ecology and Evolution, 11:910–921.

Harris LR, Holness SD (2023) A practical approach to setting heuristic marine biodiversity targets for systematic conservation planning. Biological Conservation, 285: 110218.

Jung M, Arnell A, de Lamo X, García-Rangel S, Lewis M, Mark J, Merow C, Miles L, Ondo I, Pironon S, Ravilious C, Rivers M, Schepaschenko D, Tallowin O, van Soesbergen A, Govaerts R, Boyle BL, Enquist BJ, Feng X, Gallagher R, Maitner B, Meiri S, Mulligan M, Ofer G, Roll U, Hanson JO, Jetz W, Di Marco M, McGowan J, Rinnan DS, Sachs JD, Lesiv M, Adams VM, Andrew SC, Burger JR, Hannah L, Marquet PA, McCarthy JK, Morueta-Holme N, Newman EA, Park DS, Roehrdanz PR, Svenning J-C, Violle C, Wieringa JJ, Wynne G, Fritz S, Strassburg BBN, Obersteiner M, Kapos V, Burgess N, Schmidt- Traub G, Visconti P (2021) Areas of global importance for conserving terrestrial biodiversity, carbon and water. Nature Ecology and Evolution, 5:1499–1509.

IUCN (2024). Guidelines for the application of IUCN Red List of Ecosystems Categories and Criteria, Version 2.0. Keith DA, Ferrer-Paris JR, Ghoraba SMM, Henriksen S, Monyeki M, Murray NJ, Nicholson E, Rowland J, Skowno A, Slingsby JA, Storeng AB, Valderrábano M, Zager I (Eds.). Gland, Switzerland: IUCN.

IUCN (2025) The IUCN Red List of Threatened Species. Version 2025-1. Available at https://www.iucnredlist.org. Accessed on 23 July 2025.

Polak T, Watson JEM, Fuller RA, Joseph LN, Martin TG, Possingham HP, Venter O, Carwardine J (2015) Efficient expansion of global protected areas requires simultaneous planning for species and ecosystems. Royal Society Open Science, 2: 150107.

Rodrigues ASL, Akçakaya HR, Andelman SJ, Bakarr MI, Boitani L, Brooks TM, Chanson JS, Fishpool LDC, Da Fonseca GAB, Gaston KJ, Hoffmann M, Marquet PA, Pilgrim JD, Pressey RL, Schipper J, Sechrest W, Stuart SN, Underhill LG, Waller RW, Watts MEJ, Yan X (2004) Global gap analysis: priority regions for expanding the global protected-area network. BioScience, 54: 1092–1100.

Ward M, Possingham HP, Wintle BA, Woinarski JCZ, Marsh JR, Chapple DG, Lintermans M, Scheele BC, Whiterod NS, Hoskin CJ, Aska B, Yong C, Tulloch A, Stewart R, Watson JEM (2025) The estimated cost of preventing extinction and progressing recovery for Australia's priority threatened species. Proceedings of the National Academy of Sciences, 122: e2414985122.

Watson JEM, Evans MC, Carwardine J, Fuller RA, Joseph LN, Segan DB, Taylor MFJ, Fensham RJ, Possingham HP (2010) The capacity of Australia's protected-area system to represent threatened species. Conservation Biology,25: 324–332.

Wilson KA, Meijaard E, Drummond S, Grantham HS, Boitani L, Catullo G, Christie L, Dennis R, Dutton I, Falcucci A, Maiorano L, Possingham HP, Rondinini C, Turner WR, Venter O, Watts M (2010) Conserving biodiversity in production landscapes. Ecological Applications, 20:1721–1732.

Examples

# \dontrun{
# load data
sim_pu_raster <- get_sim_pu_raster()
sim_features <- get_sim_features()

# create base problem
p0 <-
  problem(sim_pu_raster, sim_features) %>%
  add_min_set_objective() %>%
  add_binary_decisions() %>%
  add_default_solver(verbose = FALSE)

# create problem with added relative targets
p1 <- p0 %>% add_relative_targets(0.1)

# create problem with added absolute targets
p2 <- p0 %>% add_absolute_targets(3)

# create problem with added manual targets,
# and these targets equate to 10% relative targets (same as p1)
target_data <- data.frame(
  feature = names(sim_features),
  target = 0.1,
  type = "relative"
)
p3 <- p0 %>% add_manual_targets(target_data)

# create problem with added automatic targets,
# and these targets equate to 10% relative targets (same as p1)
p4 <- p0 %>% add_auto_targets(method = spec_relative_targets(0.1))

# create problem with added group targets,
# wherein the first 3 features are assigned to group A and have
# 10% targets and the remaining features are assigned to group B and
# have 20% targets
group_data <- c(rep("A", 3), rep("B", terra::nlyr(sim_features) - 3))
p5 <-
   p0 %>%
   add_group_targets(
     groups = group_data,
     method = list(
       "A" = spec_relative_targets(0.1),
       "B" = spec_relative_targets(0.2)
     )
   )

# solve problems
s <- c(solve(p1), solve(p2), solve(p3), solve(p4), solve(p5))
names(s) <- c(
  "relative targets", "absolute targets", "manual targets",
  "automatic targets", "group targets"
)

# plot solutions
plot(s, axes = FALSE)

# }

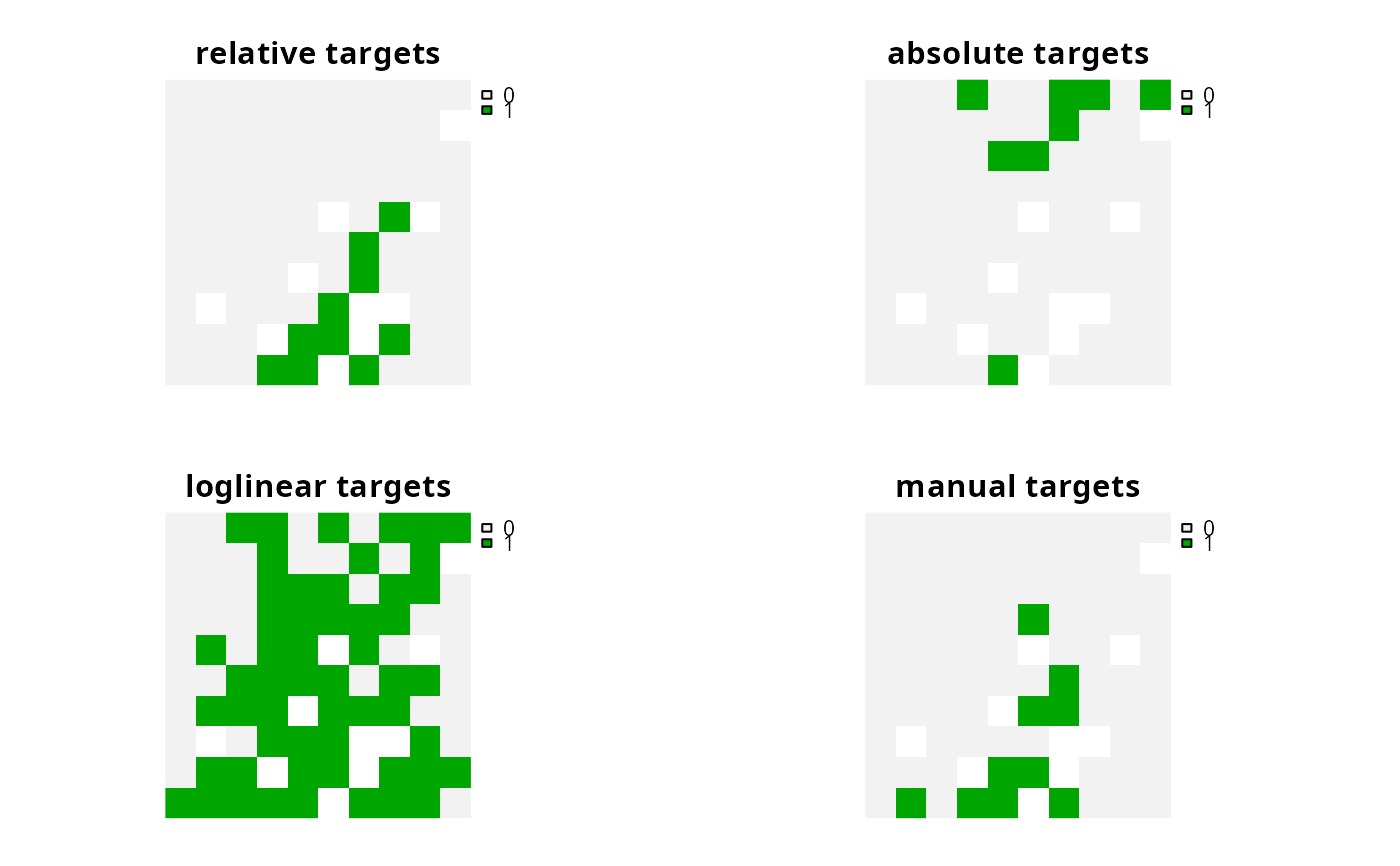Details

Target setting

Usage

References

See also

Examples