Add locked out constraints

Add constraints to a conservation planning problem to ensure that specific planning units are not selected (or allocated to a specific zone) in the solution. For example, it may be useful to lock out planning units that have been degraded and are not suitable for conserving species. If specific planning units should be locked in to the solution, use add_locked_in_constraints(). For problems with non-binary planning unit allocations (e.g., proportions), the add_manual_locked_constraints() function can be used to lock planning unit allocations to a specific value.

Usage

add_locked_out_constraints(x, locked_out)

# S4 method for ConservationProblem,numeric
add_locked_out_constraints(x, locked_out)

# S4 method for ConservationProblem,logical
add_locked_out_constraints(x, locked_out)

# S4 method for ConservationProblem,matrix
add_locked_out_constraints(x, locked_out)

# S4 method for ConservationProblem,character
add_locked_out_constraints(x, locked_out)

# S4 method for ConservationProblem,Spatial
add_locked_out_constraints(x, locked_out)

# S4 method for ConservationProblem,sf
add_locked_out_constraints(x, locked_out)

# S4 method for ConservationProblem,Raster
add_locked_out_constraints(x, locked_out)

# S4 method for ConservationProblem,SpatRaster
add_locked_out_constraints(x, locked_out)

Arguments

x: problem() object.
locked_out: Object that determines which planning units that should be locked out. See the Data format section for more information.

Value

An updated problem() object with the constraints added to it.

Data format

The locked planning units can be specified using the following formats. Generally, the locked data should correspond to the planning units in the argument to x. To help make working with terra::rast() planning unit data easier, the locked data should correspond to cell indices in the terra::rast() data. For example, integer arguments should correspond to cell indices and logical arguments should have a value for each cell---regardless of which planning unit cells contain NA values.

data as an integer vector: containing indices that indicate which planning units should be locked for the solution. This argument is only compatible with problems that contain a single zone.
data as a logical vector: containing TRUE and/or FALSE values that indicate which planning units should be locked in the solution. This argument is only compatible with problems that contain a single zone.
data as a matrix object: containing logical TRUE and/or FALSE values which indicate if certain planning units are should be locked to a specific zone in the solution. Each row corresponds to a planning unit, each column corresponds to a zone, and each cell indicates if the planning unit should be locked to a given zone. Thus each row should only contain at most a single TRUE value.
data as a character vector: containing column name(s) that indicates if planning units should be locked for the solution. This format is only compatible if the planning units in the argument to x are a sf::sf() or data.frame object. The columns must have logical (i.e., TRUE or FALSE) values indicating if the planning unit is to be locked for the solution. For problems that contain a single zone, the argument to data must contain a single column name. Otherwise, for problems that contain multiple zones, the argument to data must contain a column name for each zone.
data as a sf::sf() object: containing geometries that will be used to lock planning units for the solution. Specifically, planning units in x that spatially intersect with y will be locked (per intersecting_units()). Note that this option is only available for problems that contain a single management zone.
data as a terra::rast() object: containing cells used to lock planning units for the solution. Specifically, planning units in x that intersect with cells that have non-zero and non-NA values are locked. For problems that contain multiple zones, the data object must contain a layer for each zone. Note that for multi-band arguments, each pixel must only contain a non-zero value in a single band. Additionally, if the cost data in x is a terra::rast() object, we recommend standardizing NA values in this dataset with the cost data. In other words, the pixels in x that have NA values should also have NA values in the locked data.

Examples

# \dontrun{
# set seed for reproducibility
set.seed(500)

# load data
sim_pu_polygons <- get_sim_pu_polygons()
sim_features <- get_sim_features()
sim_locked_out_raster <- get_sim_locked_out_raster()
sim_zones_pu_raster <- get_sim_zones_pu_raster()
sim_zones_pu_polygons <- get_sim_zones_pu_polygons()
sim_zones_features <- get_sim_zones_features()

# create minimal problem
p1 <-
  problem(sim_pu_polygons, sim_features, "cost") %>%
  add_min_set_objective() %>%
  add_relative_targets(0.2) %>%
  add_binary_decisions() %>%
  add_default_solver(verbose = FALSE)

# create problem with added locked out constraints using integers
p2 <- p1 %>% add_locked_out_constraints(which(sim_pu_polygons$locked_out))

# create problem with added locked out constraints using a column name
p3 <- p1 %>% add_locked_out_constraints("locked_out")

# create problem with added locked out constraints using raster data
p4 <- p1 %>% add_locked_out_constraints(sim_locked_out_raster)

# create problem with added locked out constraints using spatial polygon data
locked_out <- sim_pu_polygons[sim_pu_polygons$locked_out == 1, ]
p5 <- p1 %>% add_locked_out_constraints(locked_out)

# solve problems
s1 <- solve(p1)
s2 <- solve(p2)
s3 <- solve(p3)
s4 <- solve(p4)
s5 <- solve(p5)

# create single object with all solutions
s6 <- sf::st_sf(
  tibble::tibble(
    s1 = s1$solution_1,
    s2 = s2$solution_1,
    s3 = s3$solution_1,
    s4 = s4$solution_1,
    s5 = s5$solution_1
  ),
  geometry = sf::st_geometry(s1)
)

# plot solutions
plot(
  s6,
  main = c(
    "none locked out", "locked out (integer input)",
    "locked out (character input)", "locked out (raster input)",
    "locked out (polygon input)"
  )
)


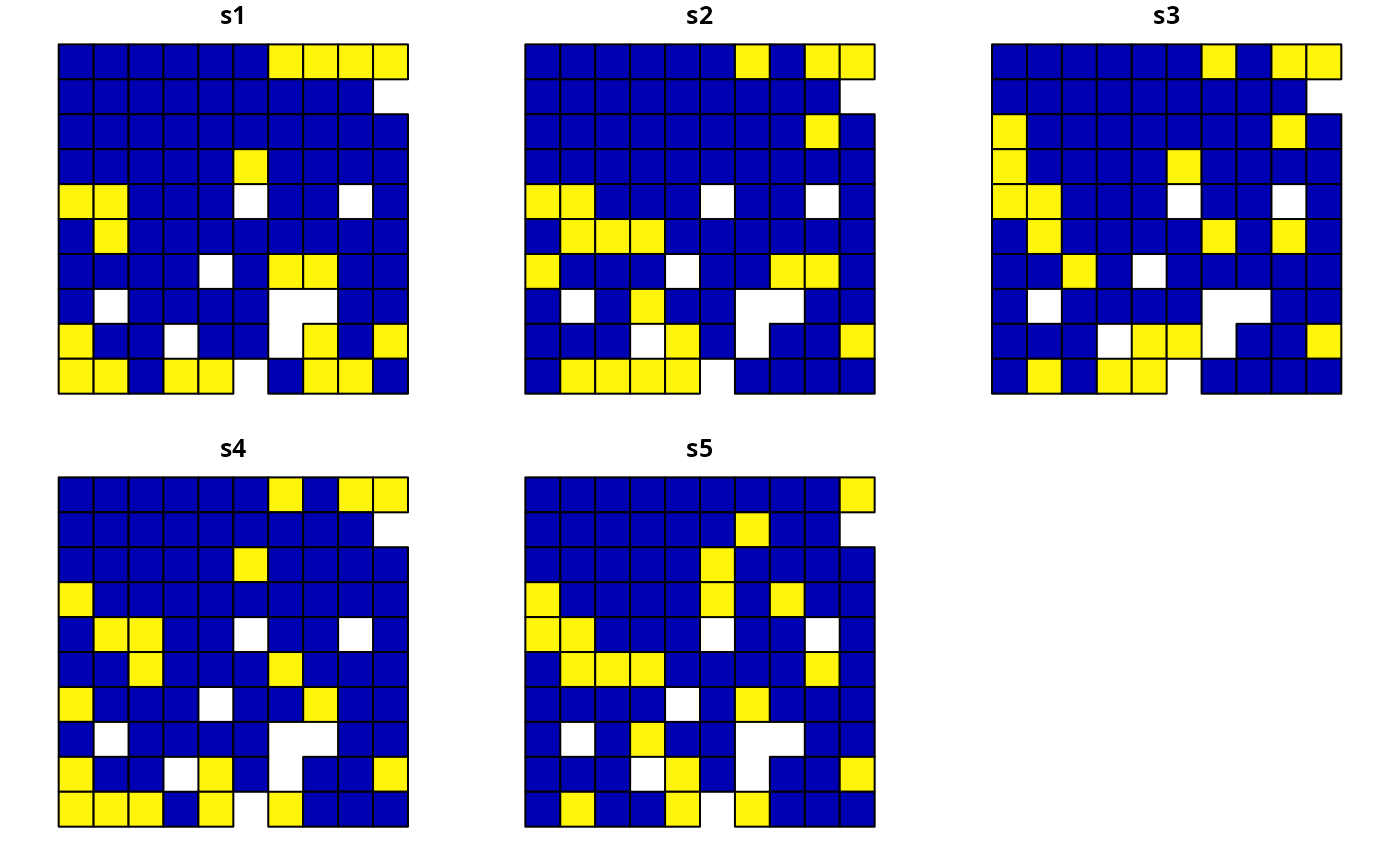# reset plot
par(mfrow = c(1, 1))

# create minimal multi-zone problem with spatial data
p7 <-
  problem(
    sim_zones_pu_polygons, sim_zones_features,
    cost_column = c("cost_1", "cost_2", "cost_3")
  ) %>%
  add_min_set_objective() %>%
  add_absolute_targets(matrix(rpois(15, 1), nrow = 5, ncol = 3)) %>%
  add_binary_decisions() %>%
  add_default_solver(verbose = FALSE)

# create multi-zone problem with locked out constraints using matrix data
locked_matrix <- as.matrix(sf::st_drop_geometry(
  sim_zones_pu_polygons[, c("locked_1", "locked_2", "locked_3")]
))

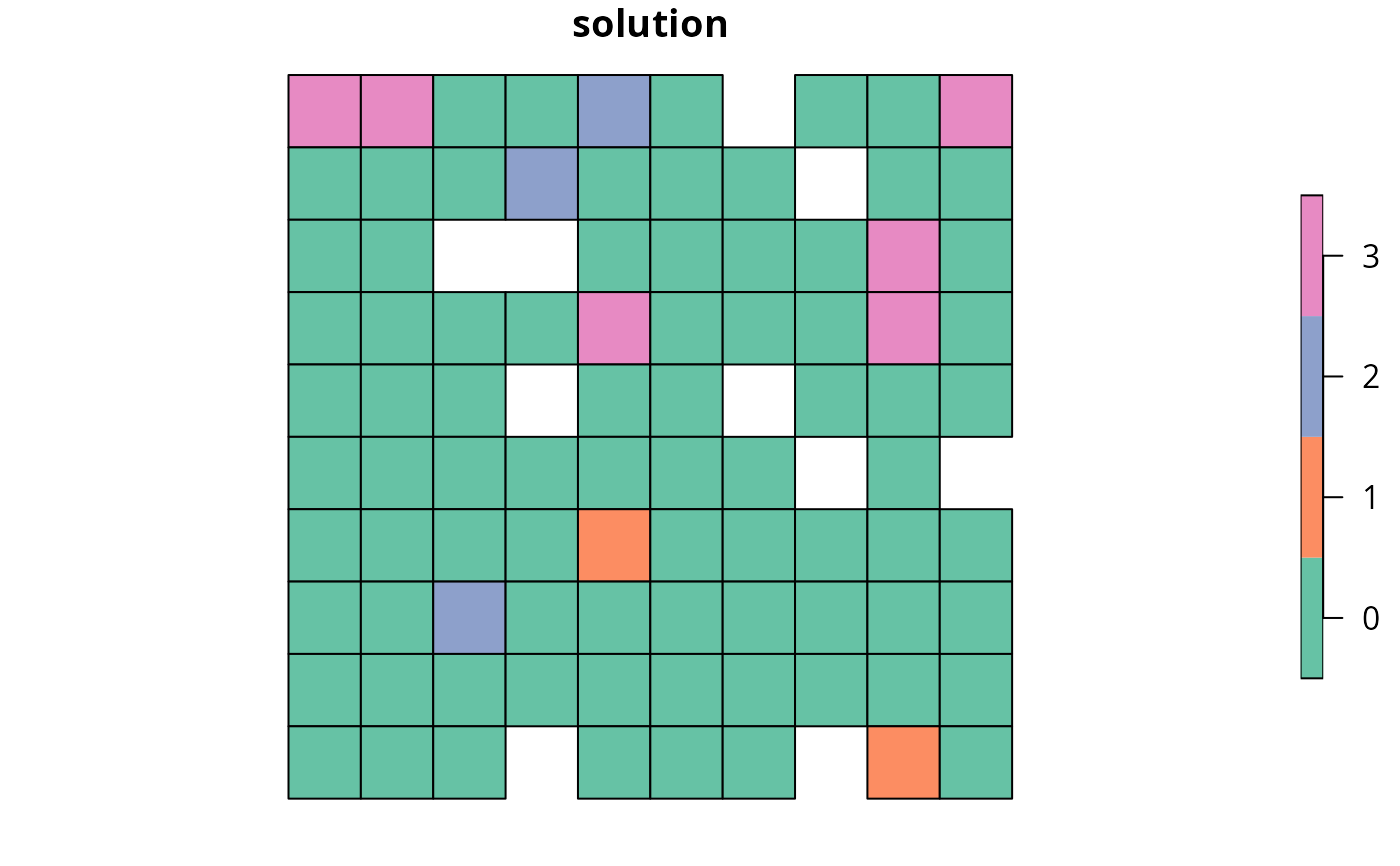
p8 <- p7 %>% add_locked_out_constraints(locked_matrix)

# solve problem
s8 <- solve(p8)

# create new column representing the zone id that each planning unit
# was allocated to in the solution
s8$solution <- category_vector(sf::st_drop_geometry(
  s8[, c("solution_1_zone_1", "solution_1_zone_2", "solution_1_zone_3")]
))
s8$solution <- factor(s8$solution)

# plot solution
plot(s8[, "solution"], main = "solution", axes = FALSE)


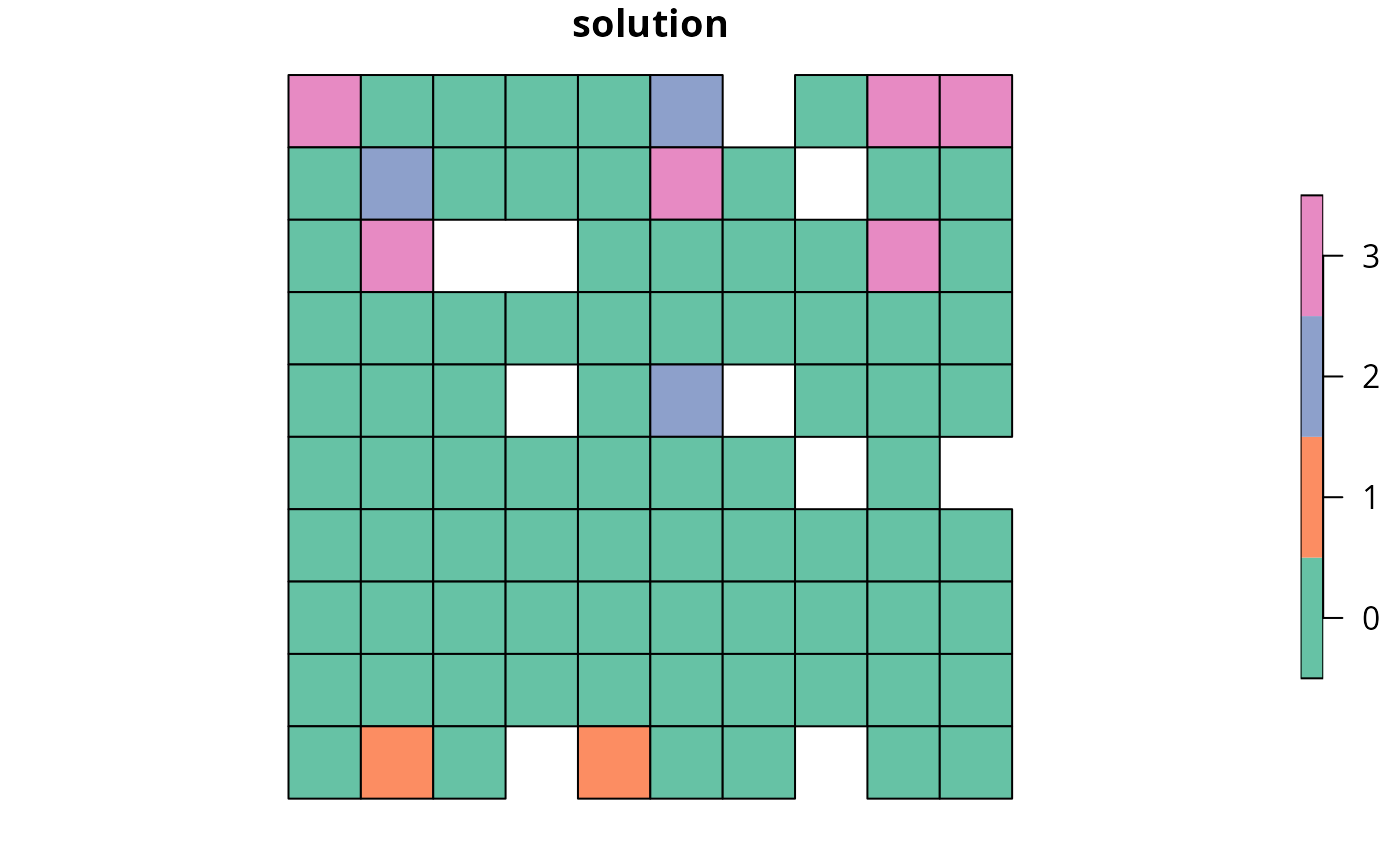
# create multi-zone problem with locked out constraints using column names
p9 <-
  p7 %>%
  add_locked_out_constraints(c("locked_1", "locked_2", "locked_3"))

# solve problem
s9 <- solve(p9)

# create new column in s8 representing the zone id that each planning unit
# was allocated to in the solution
s9$solution <- category_vector(sf::st_drop_geometry(
  s9[, c("solution_1_zone_1", "solution_1_zone_2", "solution_1_zone_3")]
))
s9$solution[s9$solution == 1 & s9$solution_1_zone_1 == 0] <- 0
s9$solution <- factor(s9$solution)

# plot solution
plot(s9[, "solution"], main = "solution", axes = FALSE)

# create multi-zone problem with raster planning units
p10 <-
  problem(sim_zones_pu_raster, sim_zones_features) %>%
  add_min_set_objective() %>%
  add_absolute_targets(matrix(rpois(15, 1), nrow = 5, ncol = 3)) %>%
  add_binary_decisions() %>%
  add_default_solver(verbose = FALSE)

# create multi-layer raster with locked out units
locked_out_raster <- sim_zones_pu_raster[[1]]
locked_out_raster[!is.na(locked_out_raster)] <- 0
locked_out_raster <- locked_out_raster[[c(1, 1, 1)]]
names(locked_out_raster) <- c("zones_1", "zones_2", "zones_3")
locked_out_raster[[1]][1] <- 1
locked_out_raster[[2]][2] <- 1
locked_out_raster[[3]][3] <- 1

# plot locked out raster
plot(locked_out_raster)


# add locked out raster units to problem
p10 <- p10 %>% add_locked_out_constraints(locked_out_raster)

# solve problem
s10 <- solve(p10)

# plot solution
plot(category_layer(s10), main = "solution", axes = FALSE)

# }

Usage

Arguments

Value

Data format

See also

Examples